3차원 물체 표현
- 폴리곤 메시 사용 - 부드러운 곡면을 근사적으로 표현
- 매개변수의 함수 사용 - 부드러운 곡면을 정확하게 표현
매개변수 곡면
CAD/CAM 분야에서 오래전부터 사용됨.
베지어 곡면: 매개변수 곡면을 표현하는 기법 중 가장 간단한 것.
베지어 곡면의 기본은 베지어 곡선이다. 이 뒷 내용으로는 베지어 곡선, 허밋 곡선에 대해 기술한다.
베지어 곡선
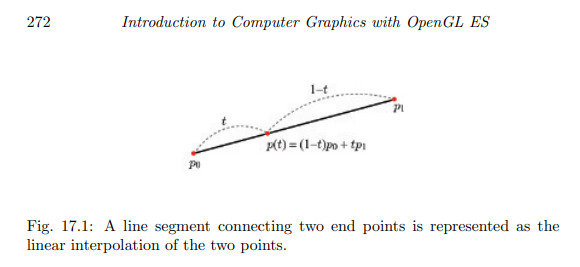
위 그림은 두 개의 끝점 p0과 p1을 잇는 선분을 보여준다.
이런 선분은 p0와 p1의 선형보간으로 표현된다.

t는 [0,1] 범위에 있으며 (1-t)와 t는 각각 p0와 p1에 대한 가중치이고, p(t)는 p0와 p1의 가중치 합이다.
세 개 이상의 점에 대해 선형보간을 재귀적으로 반복하면 베지어 곡선을 정의할 수 있는데 이를 드 카스텔조 알고리즘이라 부른다.
세 점이 주어지면 선형보간한다.

재귀적으로 선형보간을 반복하면 t의 2차 함수를 얻게 되는데, 이 것이 바로 베지어 곡선이다.

베지어 곡선을 정의하는 세 점은 컨트롤 포인트라고 부른다.
2차 베지어 곡선은 최대 1개의 변곡점을 가진다.

2차 베지어 곡선이다.

3차 이상의 베지어 곡선도 드 카스텔조 알고리즘으로 정의된다.
(a)는 세 단계의 선형보간을 통해 3차 베지어 곡선을 생성하는 절차를 보여준다.

2차 및 3차 베지어 곡선을 일반화하면 (n+1)개의 컨트롤 포인트로 n차 베지어 곡선을 정의할 수 있다. 각 컨트롤 포인트의 가중치는 매개변수 t의 다항식이다.
이를 번스타인 다항식이라고 부른다.


베지어 곡선을 렌더링하기 위해서는, 매개변수 T의 값을 조금씩 증가시켜 가면서 이에 해당하는 곡선 상의 점을 계산한 후 이 점들을 선분들로 잇는 방식을 취한다. 이 과정을 테썰레이션이라 부른다.

베지어 곡선의 특징 - 아핀 불변성
- 테썰레이션 선 수행 → 생성된 점들에 대해 아핀 변환 적용
- 아핀 변환 → 테썰레이션
결과는 동일하지만 보다 적은 수의 점에 대해 아핀 변환을 적용하는 후자가 효율적이다.

허밋 곡선과 캣멀-롬 스플라인

위 그림의 3차 베지어 곡선 함수를 t에 대해 미분하면 다음과 같은 1차 도함수를 얻는다.

이는 베지어 곡선에 접하는 접선 벡터를 나타낸다.

위 식을 다시 쓰면 다음과 같다.

베지어 곡선을 다음과 같이 바꿔 쓸 수 있다.

위 식은 두 개의 끝 점 p0와 p3, 그리고 그 점에서의 접선 벡터 v0와 v3를 사용하여 곡선 정의가 가능함을 보여준다. 이러한 곡선 표현법을 허밋 곡선이라 부른다.

- 스플라인: 복잡한 곡선은 인접한 한 쌍의 점 qi와 qi+1마다 매개변수 곡선을 정의하고 이들을 부드럽게 이어붙이는 방식으로 만들 수 있는데, 이러한 방식으로 만들어진 곡선을 스플라인이라 부른다.
접선 벡터 계산 법

r은 qi의 곡률을 결정하는데, 보통 0.5로 설정된다.
응용 사례 - 카메라 경로

카메라가 곡선 경로를 따라 움직이며 고정된 장면을 렌더링한다. 카메라 경로는 매개변수 곡선으로 묘사되며 곡선 상의 점이 EYE가 된다. AT과 UP은 각각 월드 공간의 원점과 y축으로 고정된다.
(d)에서는 동적인 카메라 공간을 사용하여 고정된 장면이 렌더링 되었다.

EYE와 AT 모두 이동한다.
(b)는 동적인 카메라 공간을 사용해 동적인 장면이 렌더링 된 모습이다.
매개변수 곡면
- 패치: 경계를 가진 곡면
→ 베지어 패치를 배울 차례
겹선형 패치 - 가장 단순한 형태의 패치.

v 방향으로 보간하면

위와 같다.

u방향의 선형보간 결과를 v방향으로 다시 선형보간 했으므로 겹선형보간을 수행한 것인데, 생성된 패치의 이름도 이를 따라 겹선형 패치라고 한다.

네 개의 컨트롤 포인트가 평면 위에 있지 않다면 겹선형 패치는 평평하지 않다.
2차 베지어 패치
겹선형 패치는 2*2 컨트롤 포인트로 정의됐다.
이것을 확장하여 3*3 컨트롤 포인트를 사용하면 2차 베지어 패치를 정의할 수 있다.
→ 우선 u방향으로 세 개씩 컨트롤 포인트를 모아 2차 베지어 곡선을 만든다.

2차 베지어 곡선 식에 특정한 u 값을 대입하면 각 곡선마다 하나의 점을 얻을 수 있다.
2차 베지어 패치는 다음과 같은 행렬 형태로 표현이 가능하다.

3*3 행렬 좌우의 행벡터와 열벡터는 각각 v와 u의 2차 번스타인 다항식들로 구성되어 있다.
위 식에서 행렬 곱셈을 완료하면 2차 베지어 패치의 식을 얻을 수 있다. (17.22 수식)
각 컨트롤 포인트의 계수는 u와 v의 번스타인 다항식이 결합된 형태인데, 이는 컨트롤 포인트에 대한 가중치 역할을 한다.

22 컨트롤 포인트마다 겹선형보간을 수행한다. 그 결과로 얻어진 22 컨트롤 포인트에 대해 다시 한번 겹선형보간을 수행한다.
3차 베지어 패치
4*4 컨트롤 포인트를 사용하면 3차 베지어 패치를 정의할 수 있다.
3차 베지어 패치는 아래와 같은 행렬 형태로 표현이 가능하다.

첫 줄의 44 행렬은 그림 (a)의 44 컨트롤 포인트와 일치한다. 이 행렬 좌우의 행벡터와 열벡터는 3차 번스타인 다항식들로 구성되었다.

3차 베지어 패치
(b)에 보인 가로 방향 곡선 4개는 모두 u의 함수로, 각각은 위 식의 4*4 행렬의 ‘행’에 기록된 컨트롤 포인트에 의해 정의된다.
(c)는 반복적 겹선형보간의 개념을 보여준다. 결과는 (b)에서 산출된 것과 동일하다. (d)는 테썰레이션 및 렌더링 결과를 보여준다.

베지어 패치는 컨트롤 포인트를 사용하여 편집된다.
컨트롤 포인트 하나가 움직일 때 곡면 모양이 상당히 변화되는 것을 볼 수 있는데, 이 것이 베지어 패치의 큰 장점이다.
베지어 삼각형
베지어 삼각형은 삼각형 구조의 컨트롤 포인트에 의해 정의되는 패치를 말한다.

세 컨트롤 포인트로 정의되는 베지어 삼각형이 (a)에 주어진다. 이를 1차 베지어 삼각형이라고 한다.
무게중심 좌표를 이용해 p = ua + ub + wc로 정의될 수 있다. 우변을 우리는 무게중심 조합이라고 부를 것이다.
베지어 삼각형으로 곡면을 표현하기 위해서는 더 많은 컨트롤 포인트가 필요하다.
다음 그림의 (a)는 삼각형 구조를 가진 6개의 컨트롤 포인트를 보여준다.
이러한 컨트롤 포인트로부터 곡면을 생성하기 위해서 반복적 무게중심 조합을 수행하자.
우선 (b)에서 색이 칠해진 세 개의 삼각형에 대해 각각 무게중심 조합을 적용한다.


그 다음에는 삼각형 <p,q,r>에 대해 또 한번 무게중심 조합을 적용한다.
결과는 (c)에서 확인할 수 있다.
2차 베지어 삼각형의 식을 얻으면 아래와 같다.


3차 베지어 삼각형은 (a)에 보인 바와 같이 10개의 컨트롤 포인트로 정의된다.
이들은 총 세 단계 반복적 무게중심 조합을 거쳐 그림 (b)의 함수를 정의한다.
이미지 출처: [OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문]
위 서적을 보고 공부한 내용을 정리함
'컴퓨터 그래픽스' 카테고리의 다른 글
| 2024.8.4(일) - 18장 GPU 테썰레이션 (0) | 2024.08.11 |
|---|---|
| 2024.7.31(수) - 16장 전역 조명과 텍스처링 (1) | 2024.08.11 |
| 2024.7.26(금) - 15장 쉐도우 매핑 (0) | 2024.08.11 |
| 2024.7.21(일) - 14장 노멀 매핑 (0) | 2024.08.11 |
| 2024.7.21(일) - 13장 캐릭터 애니메이션 (0) | 2024.07.21 |