2024.8.4(일) - 18장 GPU 테썰레이션
- 프리미티브: GPU 파이프라인이 처리하는 기하학적인 개체
- GPU 테썰레이션 지원

변위 매핑
→ 기초 표면을 고해상도 메시로 바꾼 후 그 메시의 정점 위치를 옮겨서 실제로 오돌토돌한 메시를 만든다.
변위 매핑을 위한 GPU 테썰레이션
변위 매핑 구현: 컨트롤 쉐이더 → 테썰레이터 → 생성 쉐이더

GL 3.0에서의 변위 매핑 구현은 다음과 같다.
컨트롤 쉐이더는 이 사각형 패치를 얼마나 잘게 나눌지 결정해서 테썰레이터에게 알려줘야한다.
이를 테썰레이션 레벨이라고 한다. 테썰레이터는 컨트롤 쉐이더가 지정해주는 대로 사각형 패치의 정의역을 잘게 나눠 2차원 메시를 구성한다.
- 컨트롤 쉐이더가 건네준 사각형 패치를 겹선형 패치로 간주하고 테썰레이터가 건네준 (u, v)를 사용해 사각형 패치의 한 점을 생성한다.
- GL 프로그램은 하이트맵을 생성 쉐이더에게 제공하는데, 생성 쉐이더는 이로부터 높이 값을 추출한다.
- 사각형 패치의 점을 이 높이 값만큼 수직 방향으로 올린다.
PN-삼각형

PN-삼각형을 통해 저해상도 메시를 부드러운 고해상도 메시로 바꿀 수 있다.
PN-삼각형은 메시의 한 삼각형으로부터 유도한 베지어 삼각형이라고 정의할 수 있다.
여기서 P는 point . N은 normal을 의미한다.
하나의 PN-삼각형은 테썰레이션 과정을 거쳐 다수의 작은 삼각형들을 만들고 이들은 원래의 삼각형을 대체한다.
컨트롤 포인트 계산

테두리 컨트롤 포인트를 계산한다.
입력 삼각형의 변 양 끝 정점 애트리뷰트를 이용하여 결정된다.
(c)는 베지어 삼각형의 변을 점선으로 묘사했다. 이 변은 3차 베지어 곡선이다.
(d)에 보인 것처럼, p1과 p2를 잇는 변을 3등분해서 p21과 p12를 만든다.
이 중 p21은 n1과 나란한 벡터 v21에 의해 p1의 접면으로 옮겨져서 p210이 될 것이다. (c)는 이와 마찬가지로 p12가 n2와 나란한 벡터 v12에 의해 p2의 접면으로 옮겨져서 p120이 됨을 보여주고 있다.
(d)로 돌아가 p21을 먼저 정리하자.
우선 p1에서 p2로 향하는 벡터를 3등분한다.

이렇게 구한 v1을 p1에 더하면 p21을 얻는다.

다음으로 v21을 구해야 하는데,
(18.18 그림)
위 그림에 보인 것처럼 n과 v가 둔각을 이루면 ||v||cosθ는 음수가 된다.

n1에 투영된 v1의 길이를 구하자.
그런데 n1, v1이 둔각을 이루므로 위 식의 값은 음수가 된다.
이를 양수로 바꾼 후 n1을 곱하면 벡터 v21을 얻을 수 있다.

마지막으로 p21에 v21을 더하면 p210을 얻는다.

이와 마찬가지의 방법으로 p120을 계산할 수 있다.



앞서 계산한 6개 테두리 컨트롤 포인트의 평균을 구한다.

마지막으로 E를 (E-V)/2만큼 옮겨서 p111을 결정한다.

→ 10개의 컨트롤 포인트 모두 결정 완료.
(a)에 보인 바와 같은 3차 베지어 삼각형의 식 p(u,v,w)를 얻었다.
메시를 렌더링 하기 위해서는 정점 위치만으로는 부족하다.
→ 정점 노멀이 필요함.
노멀 n1, n2, n3의 무게 중심 조합을 택해 계산 가능하다.
n(u,v,w)은 결국 {n1, n2, n3}에 기반한 1차 베지어 삼각형임.
→ 컨트롤 포인트와 대비되도록 우리는 {n1, n2, n3}를 컨트롤 노멀이라 부른다.
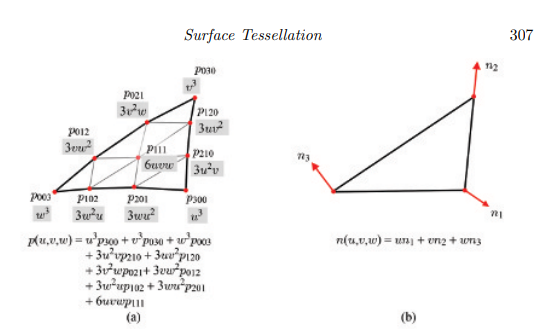
컨트롤 포인트와 컨트롤 노멀.
요약하면, 균일하게 샘플한 (u,v,w)를 그림 (a)의 p(u,v,w)에 대입해 정점 위치를 얻고,
(b)의 n(u,v,w)에 대입하여 정점 노멀을 얻는 것이다.
*하지만 현재 n(u,v,w)는 1차식이므로 문제를 야기할 수 있다.
⇒ 2차 베지어 삼각형으로 정의된 n(u,v,w)를 대안으로 제시.
컨트롤 노멀 계산
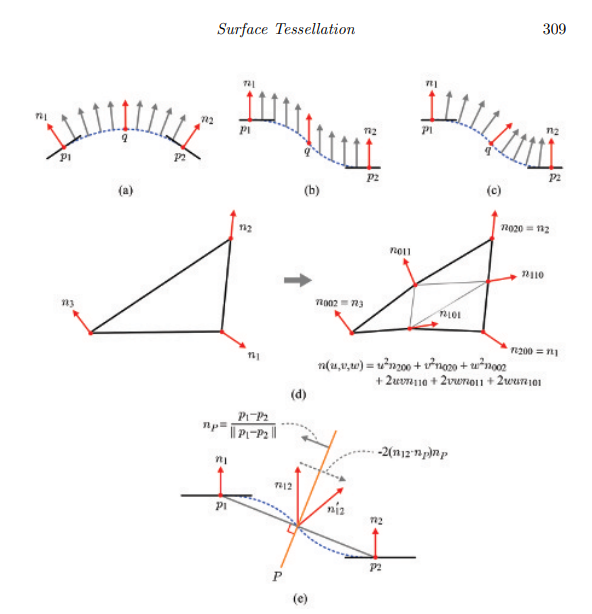
(c)는 정상적인 노멀을 제시하고 있다.
n(u,v,w)를 2차 베지어 삼각형으로 정의하면 이러한 노멀을 얻을 수 있는 것이다.
이를 위해서는 (d)에서 확인 가능하다시피 6개의 컨트롤 노멀 사용이 필요하다.
(e)는 휴리스틱 한 가지를 보여준다.
p1과 p2를 잇는 선분에 수직인 평면 P를 생각해보자. P의 노멀 nP는 다음과 같이 계산된다.

정점 노멀 n1과 n2를 더한 결과를 n12라 하면,

위와 같다.
n12를 정규화 하면 컨트롤 노멀 n110을 얻을 수 있는 것이다.
PN-삼각형을 위한 GPU 테썰레이션

컨트롤 쉐이더는 (a)와 같은 3차 베지어 삼각형 p(u,v,w)의 컨트롤 포인트를 계산한다.
(b)와 같은 1차 베지어 삼각형 n(u.v.w)를 사용하며 테썰레이션 레벨을 결정해서 테썰레이터에게 알려준다. 테썰레이터는 컨트롤 쉐이더가 지정해주는 대로 삼각형 정의역을 잘게 나눠 2차원 메시를 구성한다. 위 그림에서 볼 수 있다시피 2차원 메시는 정삼각형으로만 구성되어 있지만 실제 구현은 이와 다르다.
2차원 메시의 각 정점에 대해 생성 쉐이더가 한 번 실행되고, 컨트롤 쉐이더가 건네준 컨트롤 포인트와 컨트롤 노멀을 사용해 각각 p(u,v,w)와 n(u,v,w)를 만든 후, 테썰레이터가 건네준 (u,v,w)를 대입하여 3차원 정점의 위치, 노멀을 계산한다. 이런 방식으로 2차원 메시가 모두 처리되면, 그림 하단에 보인 바와 같은 부드러운 고해상도 메시가 생성된다. 이는 GPU 파이프라인 다음 단계로 넘겨진다.

3번 줄에서 vertice가 1로 설정된 것은, 단 하나의 컨트롤 쉐이더만 작동된다는 뜻이다.
즉 컨트롤 포인트 10개와 컨트롤 노멀 3개가 단 하나의 컨트롤 쉐이더에 의해 계산된다는 것이다.
이를 위해 10번 줄에 PNT라는 구조체가 정의되었다.

삼각형 패치를 위한 테썰레이션 레벨이다.
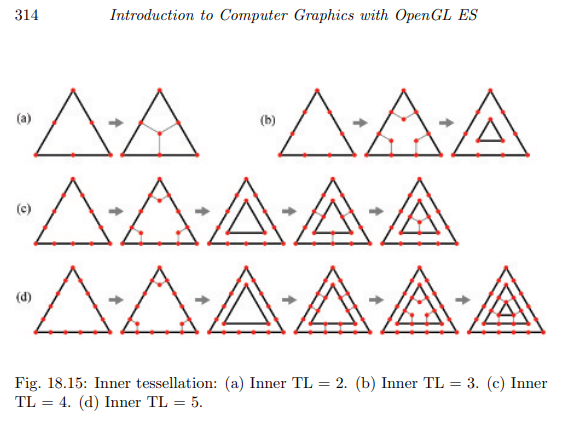
위 그림은 내부 분할을 보여준다.
(a)는 inner TL이 2로 지정되어 삼각형 정의역의 세 변이 모두 2등분 된 모습이다.
이런 방식으로 내부 분할이 완료된 후, 삼각형 정의역의 경계를 분할한다.

(a)는 inner TL과 outer TL에 의해 분할된 예를 하나 보여준다.
테썰레이터는 이렇게 분할된 정의역을 삼각형들로 채운다.
(b)를 보면, 2차원 삼각형 메시의 각 정점에는 무게중심 좌표 (u, v, w)가 할당된다.
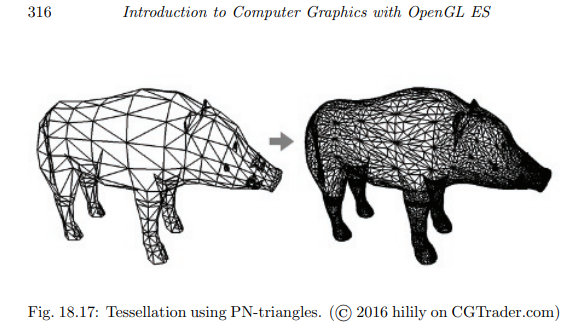
위 그림은 PN-삼각형 기반의 테썰레이션 사례를 보여준다.
이미지 출처: [OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문]
위 서적을 보고 공부한 내용을 정리함
