6.27 2장 - 수학 기초
이번 강의에서는 행렬, 벡터를 살펴보았다. 컴퓨터 그래픽스가 수학을 많이 필요로 하는 분야임이 실감난다.
이미 알고있는 것은 간단하게 정리하려 했으나 꼼꼼하게 공부하자는 의미에서 강의 내용을 정리본에 모두 포함시켰다.
행렬의 곱
A, B 두 행렬은 각각 열 크기와 행 크기가 같으므로 곱셈 가능하다.

.
2차원 벡터, 3차원 벡터
기본적으로 로우벡터라고 함.
열의 형태로 작성하면 column 벡터.

행렬*행렬 방식과 똑같이 적용 가능.
전치행렬: 어떤 행렬 M의 행, 열 바꾼 것

행렬과 벡터를 곱한 값은 행렬과 벡터를 각각 전치시킨 것의 곱과 같음.
openGL은 열 벡터, Direct3D는 행 벡터 사용함.
단위 행렬: 정사각 행렬 중 왼쪽 위 끝, 오른쪽 아래 잇는 대각선에 있는 원소가 모두 1이고 나머지 0인 행렬
역행렬: 두 정사각 행렬 A, B가 있다고 가정하면, AB = I라면
B는 A의 역행렬. 반대로 A는 B의 역행렬이 될 수 있음.


벡터
정규화: 벡터 v를 자신의 길이로 나누는 과정 --> v/||v||
단위(unit) 벡터: 길이가 1인 벡터

좌표계(공간) = 원점 + 기저
e1(1,0), e2(0,1)이면
표준기저 —> 3e1 + 5e2
표준기저X —> (3, 5) = 3(1, 1)+1(0, 2)
직교 정규(표준기저X) —> (3, 5) = 4**√2u + √2v**
2차원 공간에 있는 모든 벡터는 u, v의 선형 조합으로 나타낼 수 있음
Dot Product(= Inner Prod = 내적)
내적: n차원 벡터 a,b가 있다면 a와 b의 내적은 다음과 같이 정의된다.
1.

2. |a||b|cosΘ (Θ는 a, b 사이의 각도)
- 두 벡터 수직 이루면 내적은 0
- 예각이면 1
- 둔각일 경우는 -1
하나의 단위 벡터 자기 자신과 내적할 경우 1
Cross Product
3차원 벡터에서만 정의됨.
오른손 법칙

오른손 손가락 네 개를 a에서 b쪽 방향으로 감싸쥐면
엄지 손가락은 a * b의 방향울 가리킨다.
이 때 a * b의 길이는 a와 b에 의해 만들어지는 평행사변형의 넓이와 같다.
—> ||a*b|| - ||a||||b||sinΘ
a*b와 b*a는 길이는 같지만 반대 방향을 가리킨다.

직선 및 선형보간
p0와 p1을 잇는 무한한 직선 표현한 매개변수 방정식


t의 값에 따라 P(t)의 값이 어떻게 도출되는가?
- t = 0이면 P0
- t = 1이면 P1
- t = [0 , ∞]이면 광선
- t = [- ∞ , ∞]이면 양쪽으로 무한히 뻗는 직선
- t = [0, 1]일때는 p0와 p1을 잇는 선분. P(t)를 p0와 p1의 선형보간이라고 한다.
p0 = (x0 y0 z0)
p1 = (x1 y1 z1)

c0 = (R0, G0, B0), c1 = (R1, G1, B1)이면 선형보간된 색상은 아래와 같이 정의된다.
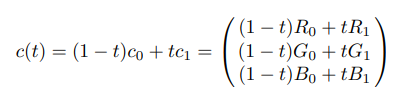
이미지 출처
[OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문]
