2024.7.20(토) - 11장 오일러 변환 및 쿼터니언
오일러 변환
세 개의 주축 중심 회전을 결합한 것.
월드 공간 오일러 변환

(a)는 주전자를 월드 공간의 x, y, x축 중심으로 순차적으로 회전시켰다.
세 축 중심의 회전각 세 개를 오일러 각이라고 한다.
오브젝트 공간 오일러 변환

위는 오브젝트 공간 오일러 변환이다.
u, v, n으로 표기한 오브젝트 공간 기저벡터를 중심으로 하는 오일러 변환

u 중심으로 θ1, 그 다음 v 중심으로 θ2만큼 회전하는 오브젝트 공간 오일러 변환은, 월드 공간 주축을 대신 사용하되 그 순서를 거꾸로 하는, 즉 먼저 y축 중심으로 θ2, 그 다음 x축 중심으로 θ1만큼 회전하는 것과 동일함.

세 가지 회전 조합으로 정의

u, v, n 순서로 오브젝트 공간 오일러 변환을 수행하는 것은, 월드 공간 주축을 대신 사용하되 그 순서를 거꾸로 해서, 즉 z, y, x축 중심으로 회전하는 것과 동일함을 알 수 있음.

주축이 아닌 임의의 축을 중심으로 하는 회전
→ 물체에 임의의 방향을 제공하는 보다 직접적인 방법
키프레임 애니메이션과 오일러 변환
- 키프레임: 60fps 애니메이션의 경우 1초에 60보다 훨씬 적은 수의 프레임에 대해서만 동작을 정의함. 이를 키프레임이라 부름.
- 중간 프레임: 키프레임 사이. 런타임에 자동으로 채워진다.
2차원 키프레임 애니메이션
- 키 데이터: 키프레임에 할당된 중요 데이터. 중간 프레임에서는 이러한 키 데이터가 보간됨.

키프레임의 위치와 방향이 보간되어 중간 프레임을 결정한다.
중간 프레임 t에서의 사각형의 위치는 다음과 같이 선형보간을 통해 결정된다.

사각형 방향도 같은 방식으로 선형보간 된다.

3차원 키프레임 애니메이션

3차원 키프레임 애니메이션은 2차원 키프레임 애니메이션과 개념적으로 동일하다.
키프레임의 위치와 방향이 보간되어 중간 프레임을 결정함.

부드러운 애니메이션은 종종 고차원 보간을 통해 얻어진다.
위 그림은 앞선 그림의 곡선을 이용해 보간한 애니메이션 결과를 보여준다.
오일러 각의 보간
물체의 방향을 정의하는 데 있어 오일러 각 (θx, θy, θz)는 매우 직관적인 수단을 제공한다. 하지만 오일러 각이 가진 문제 중 하나는 이것이 올바르게 보간된다는 보장이 없다는 사실이다.

위 그림의 (c)는 오일러 각을 연속적으로 적용한 결과를 보여준다.
보간을 핵심 기능으로 가지는 키프레임 애니메이션에는 오일러 각이 적합하지 않다. 그러나 임의의 방향이나 회전을 표현하는 또 다른 기법인 쿼터니언은 항상 올바르게 보간된다.
쿼터니언
쿼터니언 표현
쿼터니언 q는 복소수를 확장한 것으로 다음과 같이 네 개의 항으로 표현된다.
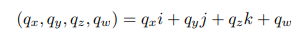
여기서 qx, qy, qz는 허수부를 구성하고, qw는 실수부.
허수단위는 다음과 같은 특징을 가진다.

두 개 서로 다른 허수단위가 곱해지면 다음과 같은 순환치환적인 특징을 가진다.

두 쿼터니언을 각각 p, q로 표기하고 이들의 곱을 계산하면 다음과 같다.

일반 복소수처럼 쿼터니언도 켤레를 가진다. q의 켤레 쿼터니언은 다음과 같다.

쿼터니언의 크기는 일반적인 벡터의 경우와 같은 방법으로 계산된다.

쿼터니언을 이용한 회전


복소수를 이용하여 2차원 회전을 표현한 것.
비슷한 방법으로 3차원 회전도 정리 가능하다.

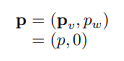
회전축 u와 회전각 θ로 또 다른 쿼터니언 q 정의.
회전을 표현하는 쿼터니언의 크기는 1이 되어야 한다.
u를 먼저 자신의 길이로 나눠 단위 벡터 u를 만들자.
그러면 크기가 1인 극형식의 쿼터니언은 다음과 같다.

마지막으로 p를 u 중심으로 θ만큼 회전하는 것은 다음과 같이 표현된다.


rq가 두 회전이 결합된 쿼터니언임을 보여준다.

u 중심 θ만큼 회전 = -u 중심 -θ만큼 회전.

쿼터니언의 보간
회전을 나타내는 두 개의 단위; 쿼터니언 q와 r을 생각해보자. 이들은 [0, 1] 범위에서 정규화된 파라미터 t를 사용해 다음처럼 보간된다.

위 식은 선형보간의 변형으로, 구체 선형보간이라 부른다.
쿼터니언과 회전 행렬

이미지 출처: [OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문]
위 서적을 보고 공부한 내용을 정리함
